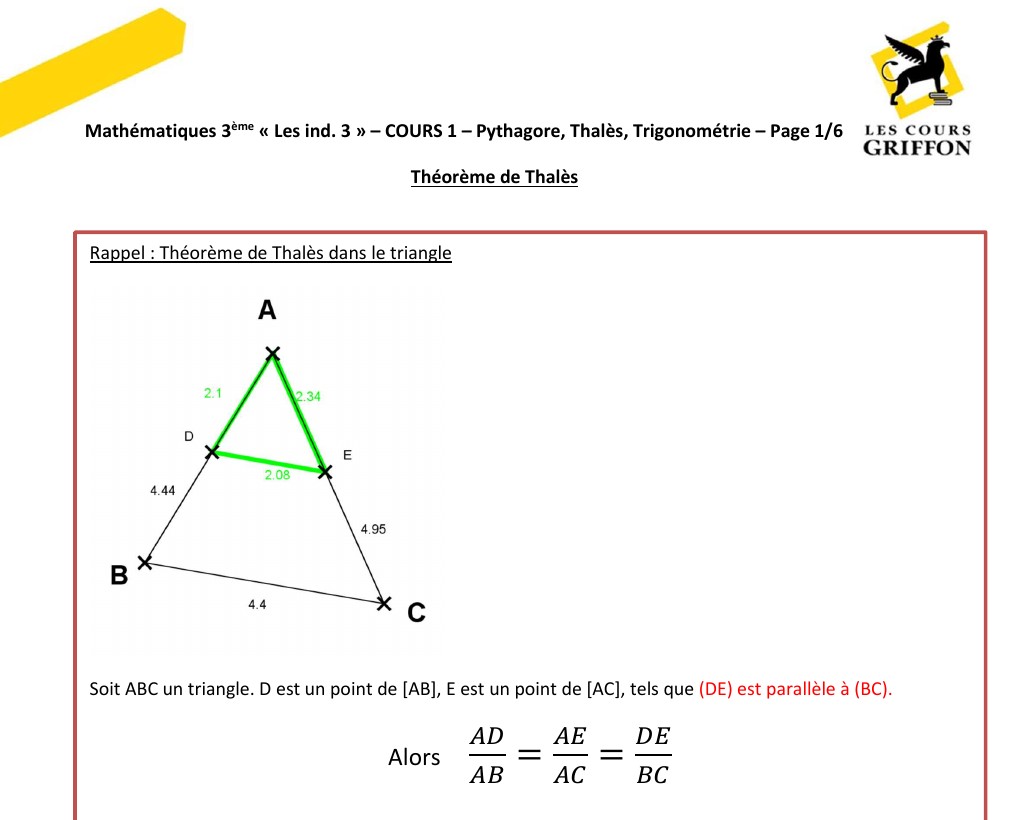
Théorème de Thalès : tout ce qu'il faut savoir
Le théorème de Thalès est un pilier incontournable de la géométrie, connu pour sa simplicité et son utilité. Ce concept repose sur les notions de proportions et de droites parallèles et constitue une solution pratique pour mesurer des distances ou établir des rapports entre des segments.
Enseigné dès le collège en classe de quatrième puis approfondi en troisième, le théorème de Thalès constitue une base solide pour comprendre des principes d’enseignement mathématiques avancés. Il découle du théorème de la droite des milieux (qui n’est malheureusement plus enseigné, à part au Cours Griffon et par quelques excellents professeurs qui s’affranchissent un peu du programme officiel.
Le Cours Griffon explore en détail ce qu’il faut savoir sur le théorème de Thalès, depuis sa définition et son origine jusqu’à ses applications concrètes, ses règles d’utilisation et sa réciproque.
Table des matières
Quelle définition retenir du théorème de Thalès ?
Le théorème de Thalès établit une règle fondamentale de la géométrie, très utilisée en maths, qui repose sur les proportions et les rapports.
Il affirme que si deux droites parallèles coupent deux droites sécantes, elles forment deux triangles dont les côtés correspondants sont proportionnels.
Dit autrement, dans une figure géométrique comme un triangle, si une droite est parallèle à l’un de ses côtés, elle divise les deux autres côtés en segments dont les longueurs suivent un même rapport.
Ce principe s’applique dans l’enseignement des mathématiques à des triangles et à d’autres configurations géométriques. Il concerne des lignes parallèles et des points alignés dans un ordre précis pour assurer la validité des proportions. Sous ces conditions, il devient un outil essentiel pour comprendre les relations de proportionnalité dans des figures géométriques et résoudre des problèmes pratiques.
Le théorème de Thalès est une base incontournable pour progresser en maths. Il s’inscrit ainsi au cœur de l’enseignement et des exercices sur les rapports et les segments dans des figures complexes.
Qui était Thalès de Milet ?
Thalès de Milet, né vers 624 av. J.-C. et mort aux environs de 548 av. J.-C., est un philosophe, mathématicien et astronome grec de l’Antiquité.
Considéré comme l’un des Sept Sages de la Grèce, il est célèbre pour avoir introduit une pensée rationnelle, rompant avec les explications mythologiques préexistantes. Il aurait prédit une éclipse solaire en 585 av. J.-C. et étudié la géométrie pour résoudre des problèmes concrets.
Père du théorème qui porte son nom, Thalès a posé les bases de la logique scientifique et de la géométrie en influençant durablement les mathématiques occidentales.
Histoire et application pratiques du théorème de Thalès
Le théorème de Thalès n’a pas été formalisé à l’époque où vivait Thalès de Milet. Ce principe géométrique, étudié et structuré plus tard par Euclide, repose sur l’idée que si une droite est parallèle à un côté d’un triangle, elle divise les deux autres côtés en segments proportionnels.
Dès l’Antiquité, Thalès aurait utilisé ce concept pour résoudre des problèmes pratiques, comme mesurer la hauteur des pyramides en Égypte à partir de points précis et d’observations linéaires.
Les applications du théorème de Thalès sont multiples et restent d’actualité encore aujourd’hui, en 2024. En topographie, il permet de mesurer des distances inaccessibles, comme la hauteur d’un bâtiment ou d’un arbre, en utilisant les proportions entre des ombres portées et des objets de référence.
Ces mesures reposent souvent sur l’égalité des rapports entre des longueurs définies par des lignes géométriques tracées sur le terrain. En cartographie, ce théorème est opportun pour représenter des distances réelles sur des cartes avec précision.
Dans l’architecture et l’ingénierie, il garantit des proportions équilibrées dans la conception de bâtiments, ponts ou autres structures. Les astronomes s’appuient également sur ce principe pour calculer la taille d’objets célestes ou déterminer des distances dans l’espace. En navigation, les marins utilisent les rapports entre des points alignés pour ajuster leurs calculs et en photographie aérienne, des lignes proportionnelles aident à redimensionner les images.
Avec ces nombreuses applications pratiques, le théorème de Thalès s’impose comme une référence intemporelle en géométrie, comme en maths. Il est donc préférable de bien comprendre comment il fonctionne pour l’utiliser correctement.
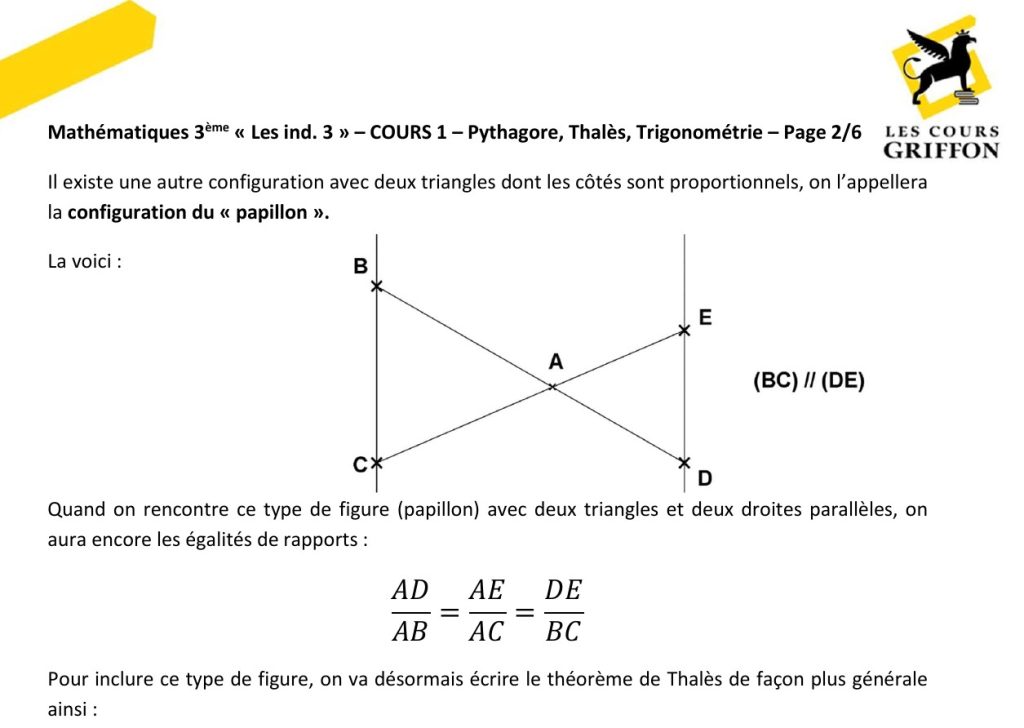
Quelles sont les règles d’application du théorème de Thalès ?
Tout d’abord, il faut la présence de deux droites parallèles qui coupent deux autres droites sécantes, c’est-à-dire des droites qui se croisent en un point. Cette configuration forme deux triangles partageant des proportions entre leurs segments. Ces triangles sont alors similaires, leurs angles étant égaux et leurs côtés proportionnels.
Pour utiliser le théorème, il importe de vérifier la configuration géométrique. Une droite doit être parallèle à un côté du triangle étudié et cette même droite doit couper les deux autres côtés du triangle en créant des segments distincts. La proportionnalité entre les longueurs des segments doit alors être calculée pour vérifier ou appliquer la règle du théorème de Thalès.
En pratique, les étapes incluent la vérification des droites parallèles, la mesure des longueurs connues et l’utilisation des rapports proportionnels pour trouver des longueurs inconnues. Dans un triangle ABC, si une droite parallèle à BC coupe les côtés AB et AC en des points distincts, les segments ainsi formés respectent un rapport constant.
Ces règles d’application assurent la fiabilité du théorème de Thalès, que ce soit pour démontrer des relations géométriques ou résoudre des problèmes concrets, comme mesurer des distances ou concevoir des figures précises en géométrie plane.
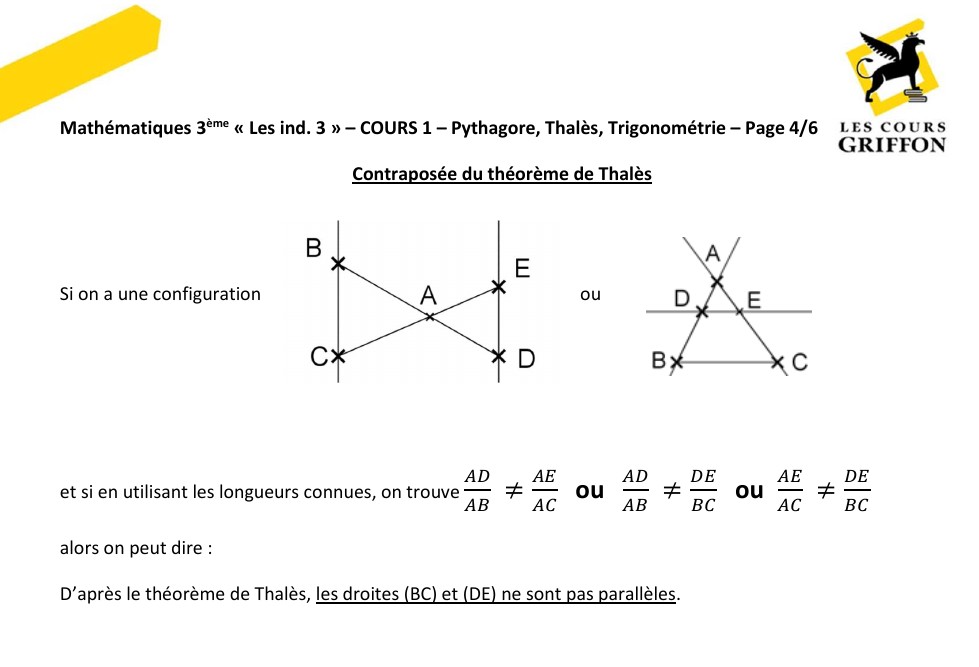
Qu’est-ce que la réciproque dans le théorème de Thalès ?
La réciproque du théorème de Thalès est une extension de ce principe géométrique qui fonctionne dans le sens inverse.
Elle permet de démontrer qu’une droite est parallèle à un côté d’un triangle en vérifiant une condition de proportionnalité. Si une droite coupe les deux autres côtés du triangle en divisant leurs segments selon un rapport constant, alors cette droite est parallèle au troisième côté.
Ce concept est utile pour prouver des propriétés géométriques sans avoir à mesurer directement les angles. À titre d’exemple, dans un triangle ABC, si une droite coupe les côtés AB et AC en formant des segments proportionnels (AD/DB = AE/EC), alors cette droite est parallèle au côté BC.
La réciproque est couramment utilisée pour valider la configuration des figures géométriques et assurer la précision des constructions. Elle renforce l’importance du théorème de Thalès dans la résolution de problèmes pratiques et théoriques en mathématiques et en géométrie.
Quand apprend-on le théorème de Thalès à l’école ?
Le théorème de Thalès est introduit dans le système éducatif français dès le collège, généralement en classe de quatrième, puis approfondi en classe de troisième.
Les élèves découvrent son énoncé et apprennent à l’appliquer dans des figures géométriques impliquant des lignes parallèles et des segments proportionnels.
À cet âge, ils développent leur compréhension des proportions, des relations entre les points et des longueurs, ce qui en fait un moment clé pour aborder ce concept. Le programme d’enseignement met l’accent sur des exercices pratiques, comme le calcul de distances ou la construction de figures, ainsi que sur la démonstration de la réciproque.
L’apprentissage du théorème de Thalès ne se limite pas à la résolution d’exercices. Il renforce chez les élèves le raisonnement logique et leur capacité à structurer une démonstration en s’appuyant sur des figures précises. Ces compétences sont déterminantes pour progresser en mathématiques et dans d’autres disciplines scientifiques.
Une maîtrise solide de ce théorème, en lien avec l’étude des segments et des longueurs dans des figures, constitue une base précieuse pour les études futures, notamment au lycée en classe de première, où il est approfondi dans des contextes d’enseignement plus complexes, notamment lors d’enseignement de spécialité en mathématiques.
Faire appel à un professeur particulier peut être une solution judicieuse pour aider un élève à surmonter ses difficultés et à consolider ses bases. Les cours individuels permettent une approche personnalisée, adaptée au rythme et aux besoins spécifiques. Dans de nombreuses matières, Cours Griffon propose un accompagnement de qualité avec des enseignants expérimentés, spécialisés dans la pédagogie.
Enseigner des concepts comme le théorème de Thalès devient plus aisé grâce à des méthodes claires et structurées qui ont fait leurs preuves. Les élèves gagnent en confiance, en compréhension et en autonomie, notamment dans l’analyse des figures géométriques et le calcul des longueurs.
Envie d’en savoir plus sur les mathématiques ? Lisez nos articles suivants :
