Théorème de Pythagore : tout ce qu’il faut savoir
Le théorème de Pythagore fait partie des notions les plus célèbres des mathématiques. Il établit une relation fondamentale entre les longueurs des côtés d’un triangle rectangle. Utilisé depuis des millénaires, il est aujourd’hui un pilier de l’apprentissage scolaire et des sciences.
Ce théorème trouve ses origines dans l’Antiquité, bien avant que Pythagore ne lui donne sa forme générale. Ses applications pratiques s’étendent de l’architecture à la navigation, témoignant de son utilité dans de nombreux domaines.
Cours Griffon vous propose aujourd’hui de vous intéresser à sa définition, son histoire, sa démonstration et ses multiples usages pratiques.
Table des matières
Quelle définition retenir du théorème de Pythagore ?
Le théorème de Pythagore établit une relation mathématique fondamentale dans tout triangle rectangle. Il affirme que le carré de la longueur de l’hypoténuse, le côté opposé à l’angle droit, est égal à la somme des carrés des longueurs des deux autres côtés.
Formellement, si les côtés d’un triangle rectangle sont notés a, b, c pour l’hypoténuse, alors a² + b² = c².
Ce principe permet de calculer une longueur inconnue dans un triangle rectangle si deux côtés sont connus. Il constitue une base essentielle pour de nombreuses applications en mathématiques et en sciences, comme pour mesurer des distances ou vérifier des angles droits.
Le théorème de Pythagore est un outil clé dès le collège, introduit avec des figures géométriques simples. Sa compréhension repose sur des notions de base comme le carré d’un nombre et la relation entre les longueurs des côtés d’un triangle rectangle.

Histoire du théorème de Pythagore
Le théorème de Pythagore, bien qu’attribué au célèbre mathématicien grec, trouve ses origines bien avant son époque. Utilisé par des civilisations anciennes comme les Babyloniens et les Égyptiens, il a été formalisé et démontré par Pythagore, devenant un pilier incontournable des mathématiques modernes.
Qui était Pythagore ?
Pythagore, né vers 570 av. J.-C. sur l’île grecque de Samos, était un philosophe et mathématicien de renom.
Fondateur de l’école pythagoricienne, il voyait les nombres comme la base de l’harmonie universelle. En plus de son théorème, il a contribué à la théorie des nombres et aux mathématiques appliquées. Sa pensée, mêlant philosophie, sciences et spiritualité, a influencé des générations de penseurs.
Pythagore a également participé activement à la diffusion de méthodes mathématiques égyptiennes, perfectionnant ses techniques pour les formaliser dans des démonstrations géométriques.
Comment Pythagore a-t-il pu prouver son théorème ?
Selon la légende, Pythagore aurait été inspiré par des observations géométriques, notamment sur les diagonales des carrés.
Il aurait démontré son théorème en découpant des figures pour prouver que la somme des aires des carrés formés sur les deux petits côtés d’un triangle rectangle équivaut à l’aire du carré de l’hypoténuse.
Pythagore aurait également étudié les méthodes des Égyptiens, utilisant des cordes nouées pour matérialiser des triangles rectangles avec des côtés de longueurs spécifiques comme 3, 4 et 5. Cette observation des triplets pythagoriciens a joué un rôle clé dans sa formalisation du théorème que nous connaissons aujourd’hui.
Comment calculer l‘hypoténuse d’un triangle rectangle ?
Calculer l’hypoténuse d’un triangle rectangle repose sur le théorème de Pythagore.
L’hypoténuse est le côté opposé à l’angle droit et aussi le plus long. Si les longueurs des deux autres côtés sont connues, il suffit d’appliquer la formule : c = √(a² + b²), où a et b sont les longueurs des deux côtés adjacents, et c représente l’hypoténuse.
Pour un triangle rectangle avec des côtés de 3 cm et 4 cm, par exemple, l’hypoténuse est égale à : c = √(3² + 4²) = √(9 + 16) = 5 cm. Cette méthode garantit un calcul précis et fiable.
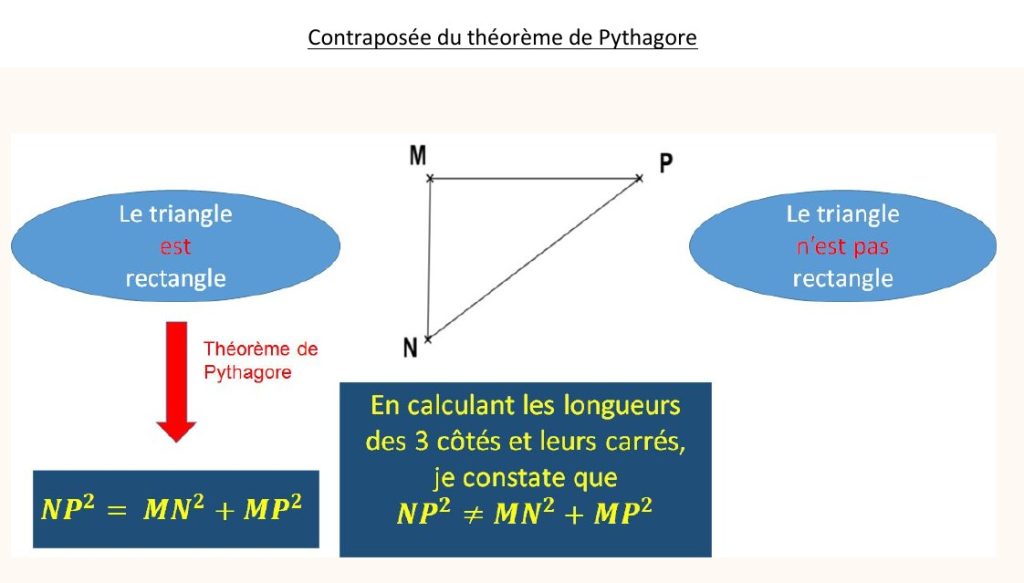
Qu’est-ce que la réciproque dans le théorème de Pythagore ?
La réciproque du théorème de Pythagore permet de vérifier qu’un triangle est rectangle. Elle précise que si le carré de la longueur du côté le plus long est égal à la somme des carrés des longueurs des deux autres côtés, alors ce triangle est un triangle rectangle.
En termes mathématiques, si c est le côté le plus long et a et b sont les autres côtés, et si c² = a² + b², alors le triangle est rectangle. Par exemple, un triangle avec des côtés de 5, 12 et 13 unités vérifie 5² + 12² = 13², soit 169, ce qui prouve qu’il est rectangle.
La réciproque du théorème est essentielle en géométrie, notamment pour construire des triangles rectangles ou vérifier des mesures dans des figures complexes.
Quelles sont les utilisations pratiques du théorème de Pythagore ?
Le théorème de Pythagore est un outil utilisé pour résoudre des problèmes pratiques dans de nombreux domaines. En architecture et en construction, il est utilisé pour vérifier les angles droits et garantir la stabilité des structures. Les ingénieurs s’en servent pour calculer les dimensions précises de bâtiments, escaliers ou ponts, en s’assurant que les angles sont parfaitement rectilignes.
Dans la navigation et la géolocalisation, ce théorème permet de calculer des distances en ligne droite entre deux points, à partir des coordonnées horizontales et verticales. Les marins, pilotes et cartographes s’appuient sur cette méthode pour établir des trajets précis.
En physique, le théorème de Pythagore est appliqué dans les calculs de trajectoires, de forces et d’énergies dans des espaces multidimensionnels. Il intervient également en astronomie pour estimer les distances entre des corps célestes ou pour analyser des phénomènes cosmiques.
Dans la vie quotidienne, il est pertinent pour mesurer des distances inaccessibles. Pour donner un exemple concret, la hauteur d’un arbre peut être estimée en utilisant son ombre et un triangle rectangle.
Enfin, en robotique et en programmation, il est utilisé pour calculer des déplacements ou des positions sur des grilles cartésiennes, ce qui facilite les opérations dans des espaces numériques.

Quand apprend-on le théorème de Pythagore ?
Le théorème de Pythagore est enseigné en classe de quatrième dans le cadre du programme de mathématiques.
Cette notion est introduite dans chaque livre de maths pour développer les compétences des élèves en géométrie, en mettant l’accent sur les triangles rectangles. À travers des exercices progressifs, ils apprennent à calculer des longueurs, vérifier des angles droits et résoudre des problèmes pratiques.
Le théorème est également utilisé comme base pour explorer d’autres concepts, comme la trigonométrie, dans les classes supérieures. Son apprentissage vise à renforcer la logique, la rigueur et l’application des mathématiques dans des contextes concrets.
Il faut bien l’avouer : comprendre le théorème de Pythagore peut être complexe pour certains élèves, notamment lorsqu’il s’agit d’appliquer des concepts comme les longueurs au carré ou la racine carrée. Un professeur particulier peut nettement aider à clarifier ces notions grâce à un accompagnement personnalisé et des explications adaptées au niveau de l’élève.
Avec le Cours Griffon, les élèves bénéficient d’un cadre pédagogique structuré et d’une méthode éprouvée pour progresser rapidement. Les enseignants qualifiés utilisent des exercices ciblés et des exemples concrets pour illustrer le théorème et ses applications pratiques.
Cette approche renforce la confiance des élèves en mathématiques et leur permet d’acquérir des bases solides. En travaillant avec des professionnels engagés, chaque élève peut ainsi surmonter ses difficultés et exceller dans cette discipline fondamentale.
Envie d’en savoir plus sur les mathématiques ? Lisez nos articles suivants :
